第一台計算機 model K,是如何用繼電器來達到計算?
前言
最近在研究半導體相關的活動,研究到邏輯閘的部分,看到了一個滿有趣的故事,看到當時貝爾實驗室的 George Stibitz 用繼電器開發出了第一台計算機 model K,聽說會取這個名字是因為 George Stibitz 是利用空閒時間,在廚房裡面所組裝出這個計算機。
讓我想到先前老黃在開箱新一代的 nvidia 顯卡,也是從在廚房裡面拿出新的顯示卡,似乎有致敬的感覺。
簡介
後來在研究這段歷史,其實 George Stibitz 做的事情,核心是將二進位的數學,轉換成邏輯的方式呈現,像是 George Stibitz 做出的二進位半加法器,其實是用電路的邏輯閘組出將和 (Sum) 跟 進位 (Carry) 的功能的電路。
像是:在兩個一位元二進位數相加時,總共會有四種可能,三個結果
如果換成二進位的話,可以表示成:
從中會發現其規律,二進位的 Curry (進位) 則是兩個數字都要為 1 時,才會輸出 1,不然其他情況下都是 0,
這個就是邏輯閘中的 AND,真值表如下所示。
這邊可以看成是兩個繼電器串聯,就可以要兩個繼電器都打開,才能讓店通過,因此透過兩個繼電器就可以達成通電的效果。
而 Sum (第一個位數) ,如果如果兩個一位元的數字中,有任何一個數字是 1 的話,則這個位數會出現 1 ;或者是只要有兩個位數相同時就會出現 0,
這個就是邏輯閘中的 XOR,真值表如下所示。
透過繼電器的交錯的連接方式,就可以達到這個效果。
從上面的例子,可以知道電腦的計算核心,是透過不同邏輯閘的電路(不同邏輯閘的組合方式),來達到計算的功能。後續也可以用相同的邏輯方法,組出來特定功能的計算機電路。
構造
這次也趁著假日,透過繼電器組出了三個一位元二進位數的全加法器,總共使用了八個繼電器,
全加法器的邏輯閘如下所示,其實就是兩個半加法器,再透過並聯達到 OR 的效果。
全加法器的邏輯閘
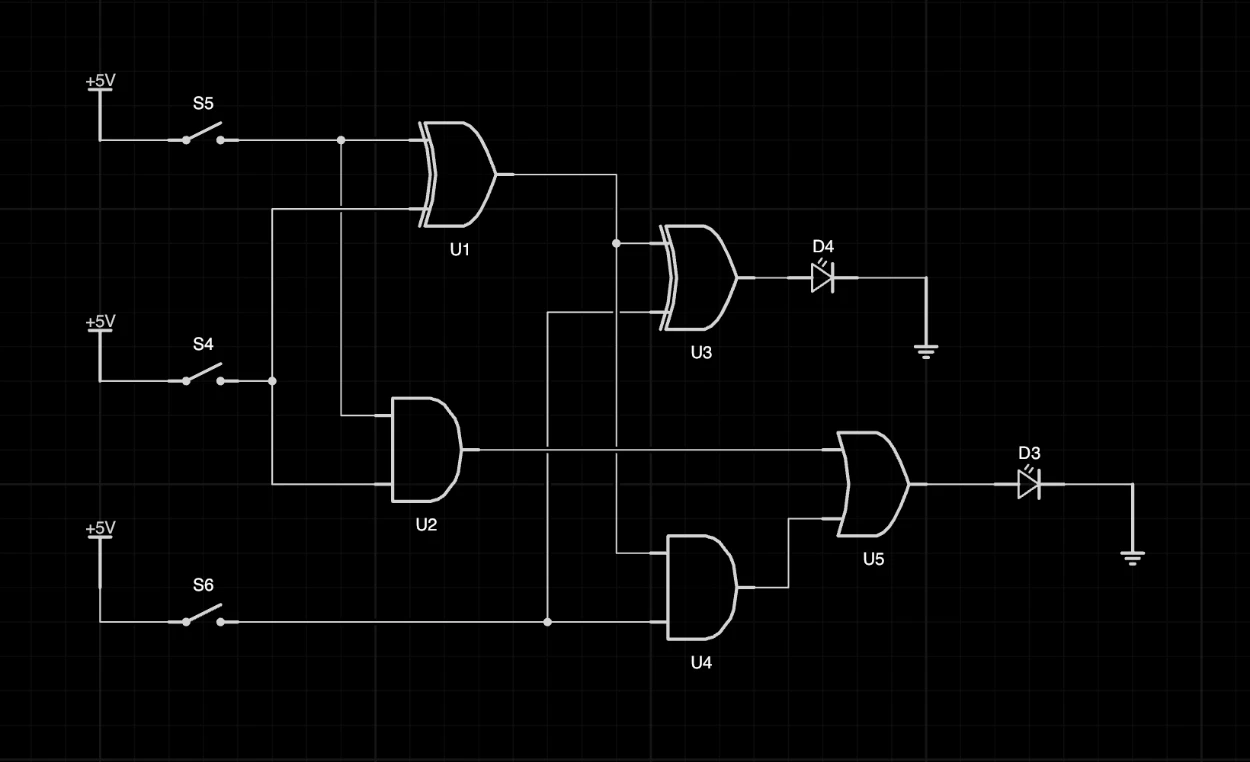
全加法器的電路圖
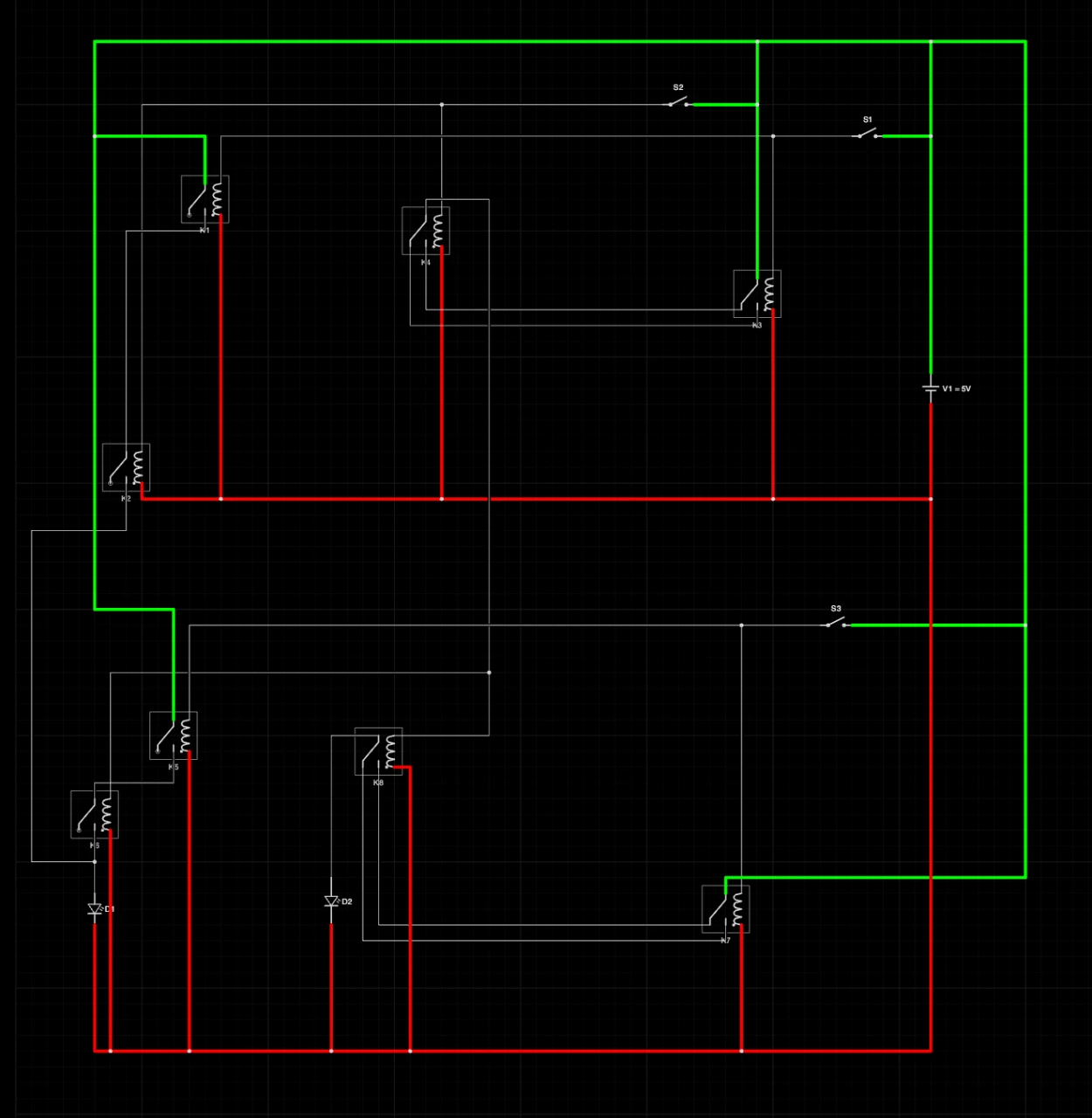
全加法器的實際電路演示
實際做到的效果:
這個裝置上面有兩個燈,綠燈代表 20 ,藍燈代表 21
- 當只有打開一個開關的時候,綠燈會發光,代表是 20,也就代表是 1。

- 當打開兩個開關的時候,藍燈會發光,代表是 21,也就代表是 2。

- 最後三個開關都打開時,綠燈與藍燈都會發光,代表是 20+21,也就代表是 3。

下面是實際的演示影片。